高等数学-学习算法/人工智能/大数据的第一步

集合与运算

集合

集合概念的引入

一个书柜中的书构成一个集合
一间教室里的全体学生构成一个集合
全体实数构成一个集合

集合的概念

集合：具有某种特定性质的事物的总体。

组成这个集合的事物称为该集合的元素。

$a \in M, a \notin M$

$\in$表示属于，$\notin$ 表示不属于

A = {a₁,a₂, … , a_n} 列举法

M = {x|x 所具有性质 P} 描述法

例：$B = \{x|x \in R, x^2 – 1 = 0\}$ → B = {-1, 1}

数集分类：

N —- 自然数集 N ={0，1，2, …, n, …}

Z —- 整数集 Z = {…, -n ,…, -2, -1, 0, 1, 2…, n,…}

Q —- 有理数集 Q = {$p \over q$|p $\in$ Z, q $\in N^+$ 且 p,q 互质}

R —- 实数集 R = {x|x 是有理数或无理数}

子集：若x $\in$ A，则必x $\in$ B，就说 A 是 B 的子集，记作 A $\subset$ B.。

数集间的关系：N $\subset$ Z，Z $\subset$ Q，Q $\subset$ R

集合相等

集合相等：若A $\subset$ B，用B $\subset$ A，就称为集合 A 与 B 相等

例： A = {1, 2}， B = {x|x² – 3x + 2 = 0}，则 A = B

空集

空集：不含任何元素的集合称为空集，记作$\varnothing$

例：{x|x $\in$ R, x² + 1 = 0} = $\varnothing$

规定空集是任何集合的子集

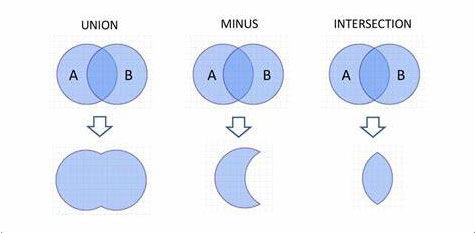
集合的运算

并集

并集：设 A 和 B是两个集合，由所有属于 A 或者属于 B的元素组成的集合，称为 A 与 B 的并集，记作 A $\cup$ B

A$\cup$B = {x| $\in$A或x$\in$B}

交集

交集：设 A 和 B是两个集合，由所有既属于 A 又属于 B的元素组成的集合，称为 A 与 B 的交集，记作 A $\cap$ B

A$\cap$B = {x| $\in$A且x$\in$B}

差集

差集：设 A 和 B是两个集合，由所有属于 A 而不属于 B的元素组成的集合，称为 A 与 B 的差集，记作 A\B，即

A\B = {x| $\in$A且x$\notin$B}

全集和补集

全集：我们研究某个问题限定在一个大的集合 I 中进行，所研究的其他集合 A 都是 I的子集，我们称集合 I 为全集。

补集：I/A 为 A 的补集，记作 A^c

例：A = {x|0 < x ≤ 1}的补集是A^c = {x|x ≤ 0或 x > 1}

区间与邻域

区间

区间：是指介于两个实数之间的全体实数。这两个实数叫做区间的端点。

$\forall$a,b $\in$ R，且 a < b

{x|a < x < b}，称为开区间。记作(a,b)

{x|a ≤ x ≤ b}，称为闭区间。记作[a,b]

{x|a ≤ x < b}，称为半开区间。记作[a,b)

{x|a < x ≤ b}，称为半开区间。记作(a,b]

无限区间

[a,+∞) = {x|a ≤ x} (-∞,b) = {x, x < b}

注：全体实数的集合 R 可以记作(-∞, +∞)

邻域

领域：设δ是任一正数，则开区间(a – δ, a + δ)就是 a 的一个邻域，这个邻域称为点 a 的δ邻域，记作 U(a, δ)，即

U(a, δ) = {x|a – δ < x < a + δ}

点 a 称为这个邻域的中心，δ称为这个邻域的半径。

由于 a – δ < x < a + δ ⇔ |x – a| < δ

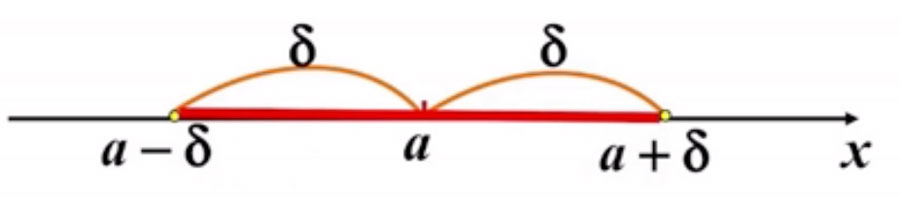
因此 U(a, δ) = {x|a – δ < x < a + δ} ⇔ U(a, δ) = {x||x – a| < δ}

U(a, δ)表示与点 a 距离小于δ的一切 x 的全体

去心邻域：U_δ(a) = {x|0 < |x – a| < δ}
左δ邻域：(a-δ, a)
右δ邻域：(a, a+δ)

机器学习中集合的应用

实例的集合
候选假设的集合
训练样例的集合

映射与函数

映射

映射的定义

定义：

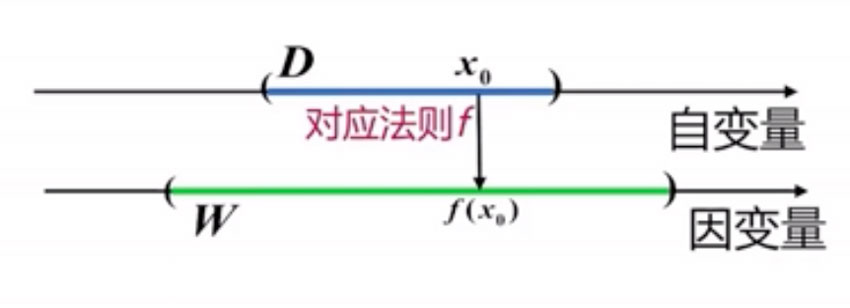
设 X, Y 是两个非空集合，如果存在一个法则 f
使得对 X 中每个元素 x，按法则 f，
在 Y 中有唯一确定的元素 y 与之对应，
则称 f 为从 X 到 Y 的映射，记作：f:X → Y。
无素 y 称为 x 的像，元素 x 称为元素y 的一个原像。

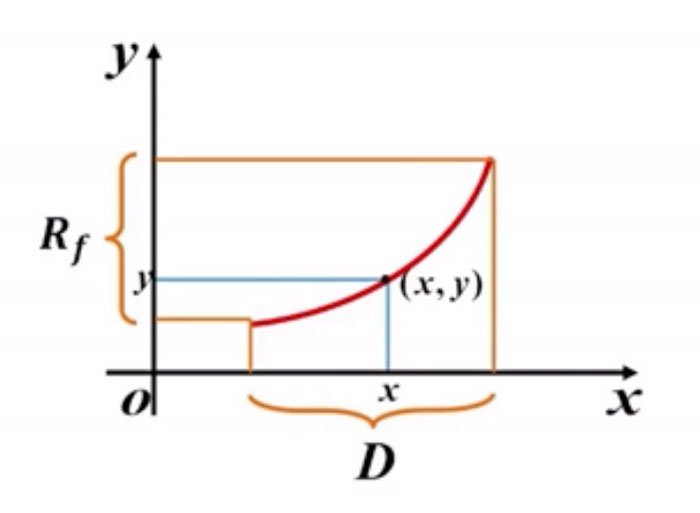
定义域：集合 X称为映射 f 的定义域，记作 D_f，即D_f = X

值域：X 中所有元素的像组成的集合称为映射 f 的值域，记作R_f 或 f(X)，即

R_f = f(X) = {f(x)|x $\in$ X}

映射三要素

集合 X，即定义域D_f = X
集合 Y，即值域的范围，R_f $\subset$ Y
对应法则 f，使用每个x $\in$ X，有唯一确定的 y = f(x)与之对应

注意

对每个 x ∈ X，元素 x 的像y 是唯一的
而对每个 y ∈ R_f，元素 y 的原像不一定是唯一的
映射 f 的值域R_f是 Y 的一个子集，即R_f $\subset$ Y，不一定R_f= Y

例题

例设 f:R → R，对每个 x ∈ R，f(x) = x²

解：显然，f 是一个映射，f 的定义域D_f= R,

值域R_f = {y|y ≥ 0}，它是 R 的一个真子集，

对于R_f中的元素y，它的原像不是唯一的。如 y =4的像就有 x = 2和 x = -2两个。

例设 f:$[-{\pi\over2},{\pi\over2}]$ → [-1,1]，对每个 x ∈ $[-{\pi\over2},{\pi\over2}]$，f(x) = sinx。

解：显然，f 是一个映射，f 的定义域D_f = $[-{\pi\over2},{\pi\over2}]$，值域R_f = [-1,1]。

满射：R_f = Y
单射：∀x₁,x₂ ∈ X，x₁≠ x₂，有 f(x₁) ≠ f(x₂)
一一映射：满射+单射

函数的概念

函数的定义

设数集 D $\subset$ R，则称映射 f: D → R 为定义在 D 上的函数，通常简记为y=f(x), x ∈ D,
其中 x 称为自变量，y 称为因变量，D 称为定义域，记作D_f，即D_f = D。

函数的概念

函数值：对于每个x ∈ D，按对应法则 f，总有唯一确定的值 y与之对应，这个值称为函数 f 在 x 处的函数值，记作 f(x)。
函数关系：因变量 y 与自变量 x 之间的这种依赖关系称为函数关系。
值域：函数值 f(x)全体构成的集合称为函数 f 的值域，记作R_f或f(D)。

函数的两要素

定义域与对应法则

函数的定义域

有实际意义背景的函数，根据实际背景中变量的实际意义确定。
例：自由落体运行$s = {1\over2}gt^2, t\in[0,T]$
抽象的用算式表达的函数，其定义域是自变量所能取的使用算式有意义的一切实数值。
例：$y = \sqrt{1-x^2}$ D:[-1,1]
$y = {1\over\sqrt{1-x^2}}$ D:(-1,1)

函数的图形表示方法

坐标平面上的点集{P(x,y)|y = f(x),x ∈ D}，称为函数 y=f(x)，x ∈ D的图形。

特殊函数举例

符号函数
$$y = sgn\ x = \begin{cases}
1\ \ \ \ 当 x>0\\
0\ \ \ \ 当 x=0\\
-1\ 当 x<0
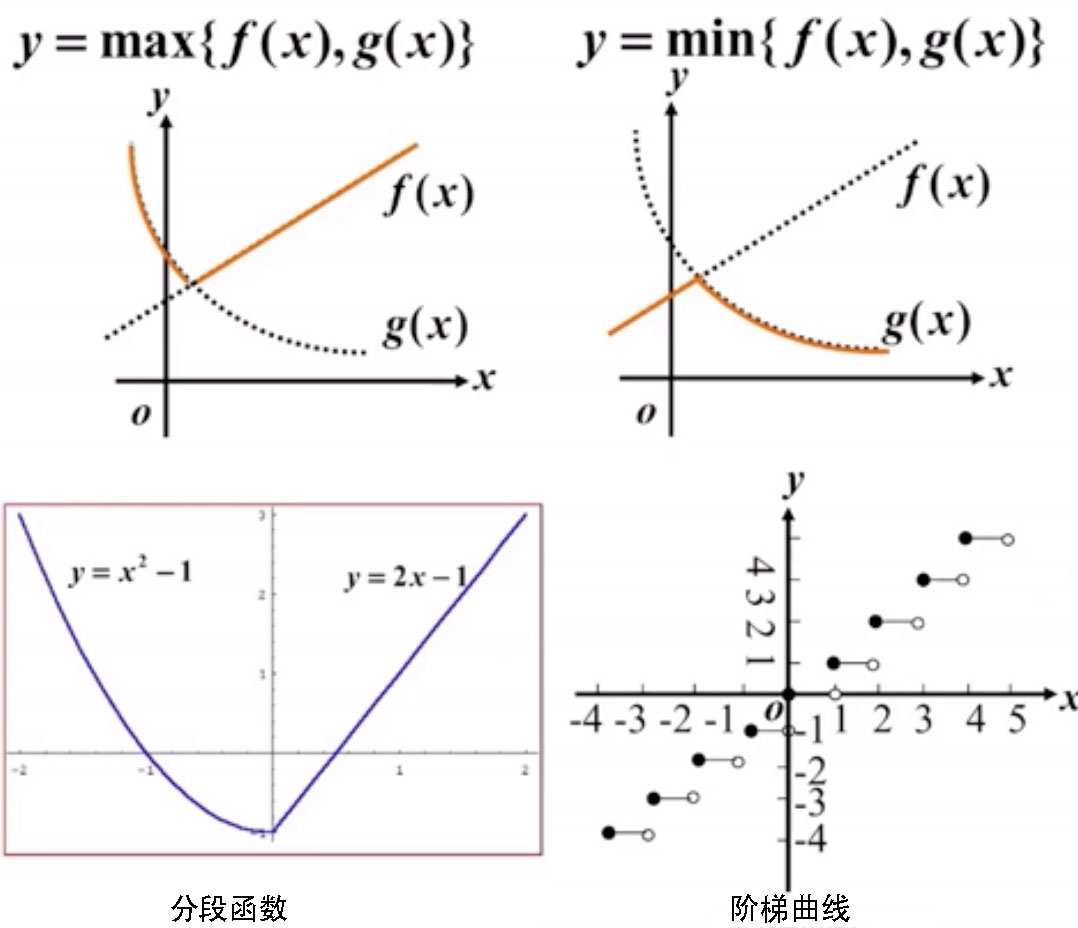
\end{cases} $$
取整函数（阶梯曲线）
y = [x], [x]表示不超 x 的最大整数
取最值函数
y = max{f(x), g(x)}
y = min{f(x), g(x)}
分段函数
在自变量的不同变化范围中，对应法则用不同的式子来表示的函数，称为分段函数
$$f(x) =\begin{cases}
2x – 1, x > 0\\
x^2 – 1, x \leq 0
\end{cases} $$

例题

例已知函数$y = f(x) =\begin{cases}
2 \sqrt x,\ 0 \geq x \leq 1\\
1 + x,\ x > 1
\end{cases}$ 求$f({1\over2})$及$f({1\over t})$，求写出定义域及值域。

解： $f({1\over t})=2\sqrt{1\over2}=\sqrt2$

$y = f(x) =\begin{cases}
1 + {1\over t},\ 0 < t < 1\\
{2 \over \sqrt t},\ t \geq 1
\end{cases}$

定义域：D = [0, +∞)

值域：f(D) = [0, +∞)

函数的特性

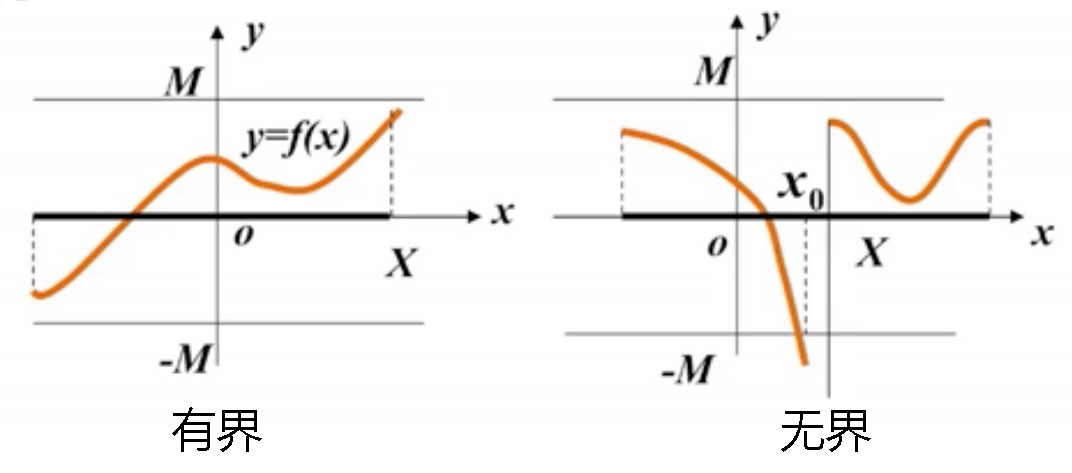
函数的有界性

若 X ⊂ D，∃M > 0，∀x ∈ X，有|f(x)| ≤ M 成立，则称函数 f(x)在 X 上有界，否则称无界。

函数的单调增加性

单调增加性

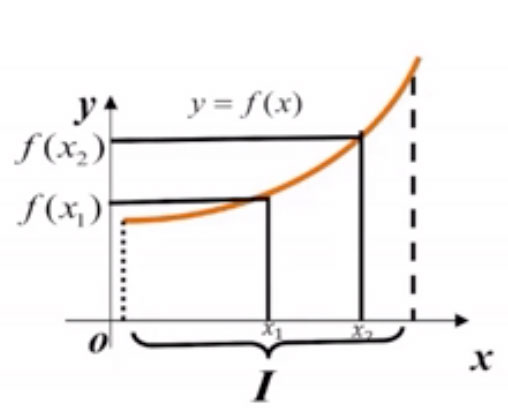
设函数 f(x)的定义域为 D，区间 I ⊂ D，
如果对于区间 I 上任意两点 x₁及 x₂，
当 x₁< x₂时，恒有 f(x₁) < f(x₂)，

则称函数 f(x)在区间 I 上是单调增加的。

函数的单调减少性

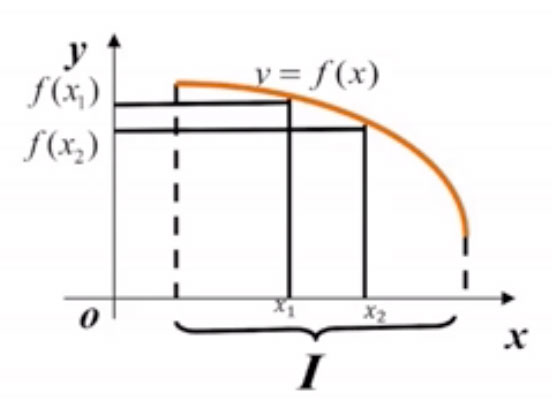
设函数 f(x)的定义域为 D，区间 I ⊂ D，
如果对于区间 I 上任意两点 x₁及 x₂，
当 x₁< x₂时，恒有 f(x₁) > f(x₂)，

则称函数 f(x)在区间 I 上是单调减少的。

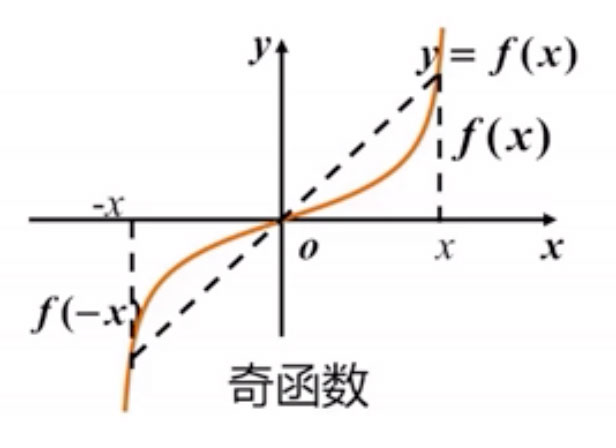
函数的奇偶性

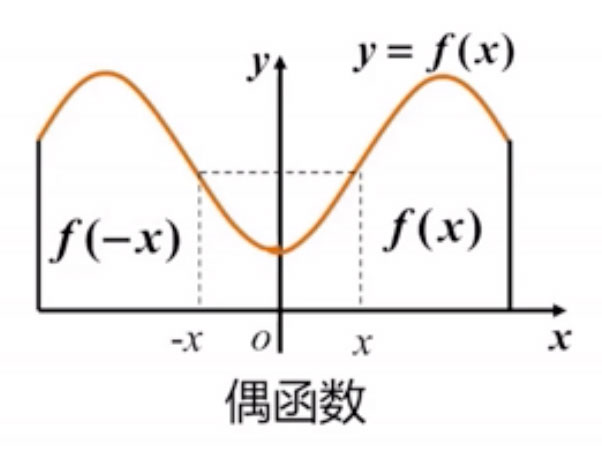
设 D 关于原点对称。
对于∀x ∈ D，有f(-x) = f(x)，

则称函数 f(x)为偶函数。

设 D 关于原点对称。
对于∀x ∈ D，有f(-x) = -f(x)，

则称函数 f(x)为奇函数。

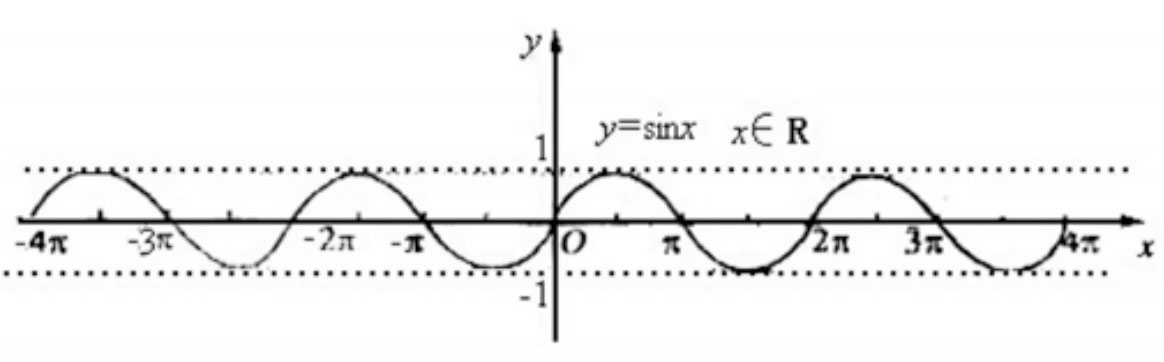
函数的周期性

设函数 f(x)的定义域为 D，如果存在一个不为零的数 l,使用对于任一x ∈ D, (x ± l) ∈ D，且 f(x+l) = f(x)恒成立，则称 f(x)为周期函数，l 称为 f(x)的周期。

通常说周期函数的周期是指其最小正周期。

初等函数

幂函数 y = x^µ（µ是常数）

指数函数 y = a^x（a > 0，且 a ≠ 1）

对数函数 y = log_ax（a > 0且 a ≠ 1），当 a = e 时，记为 y = lnx。

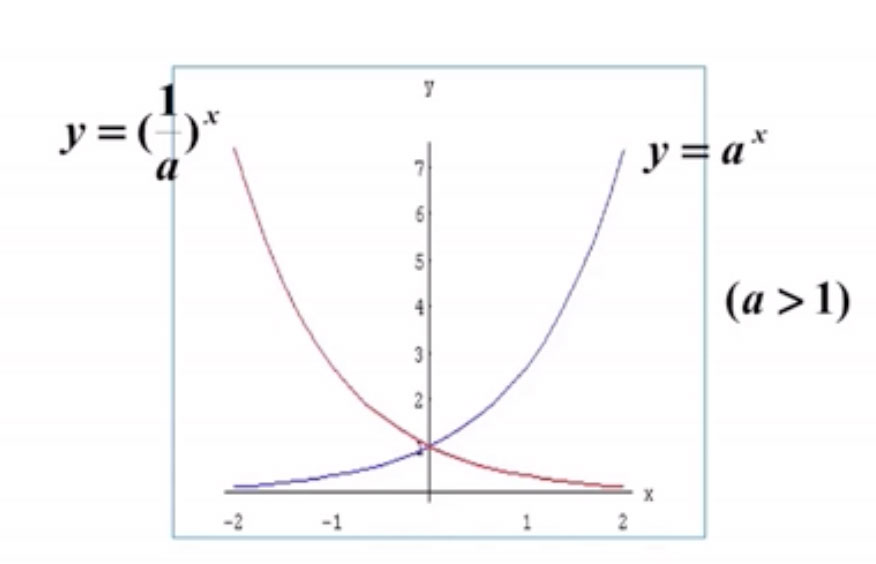
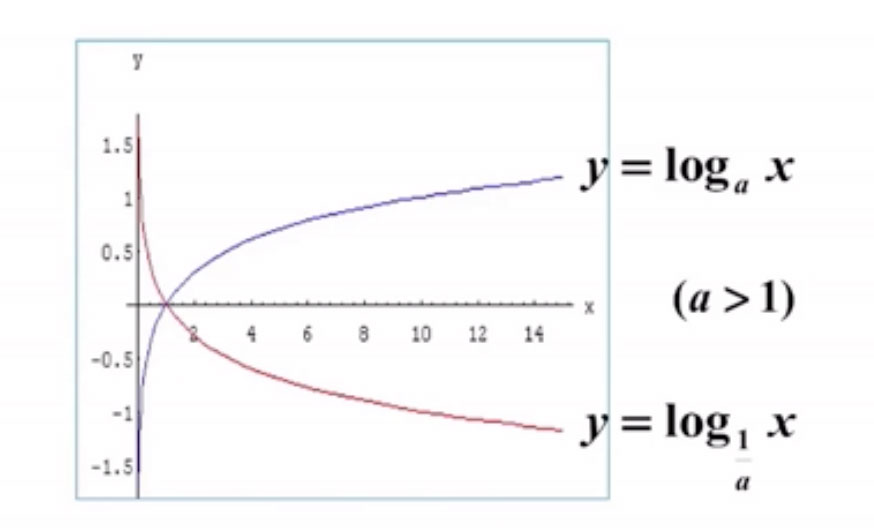
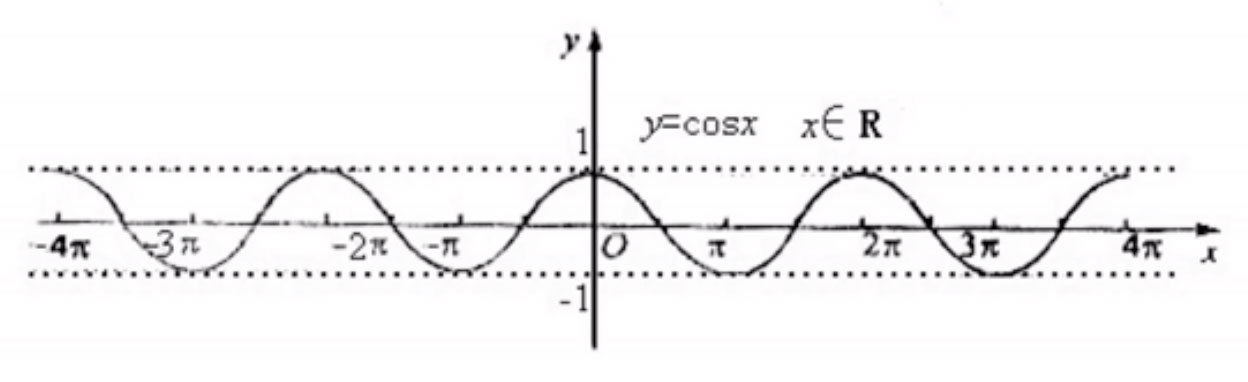
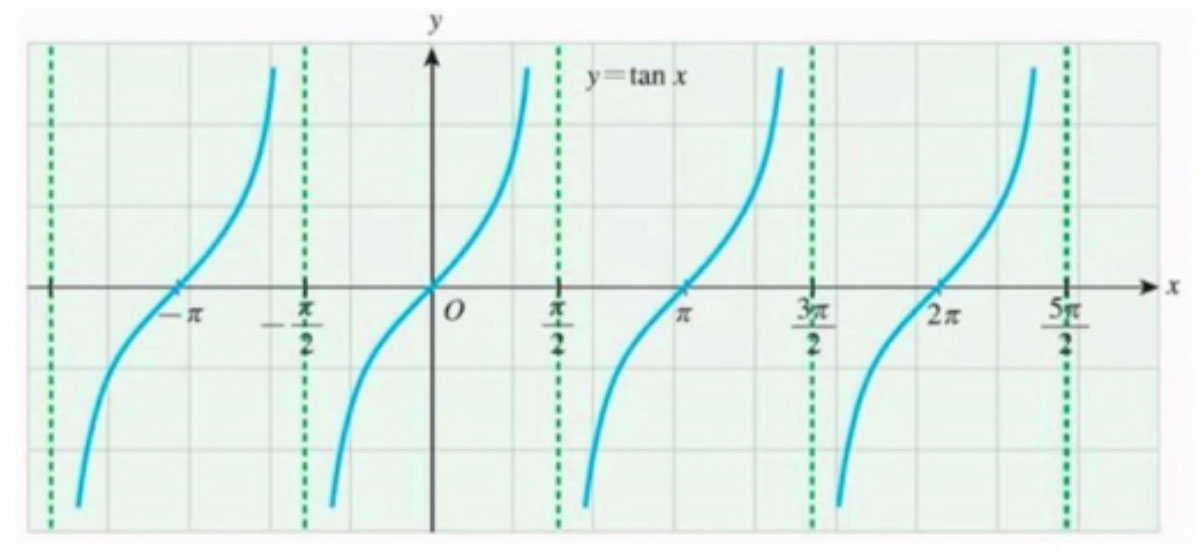
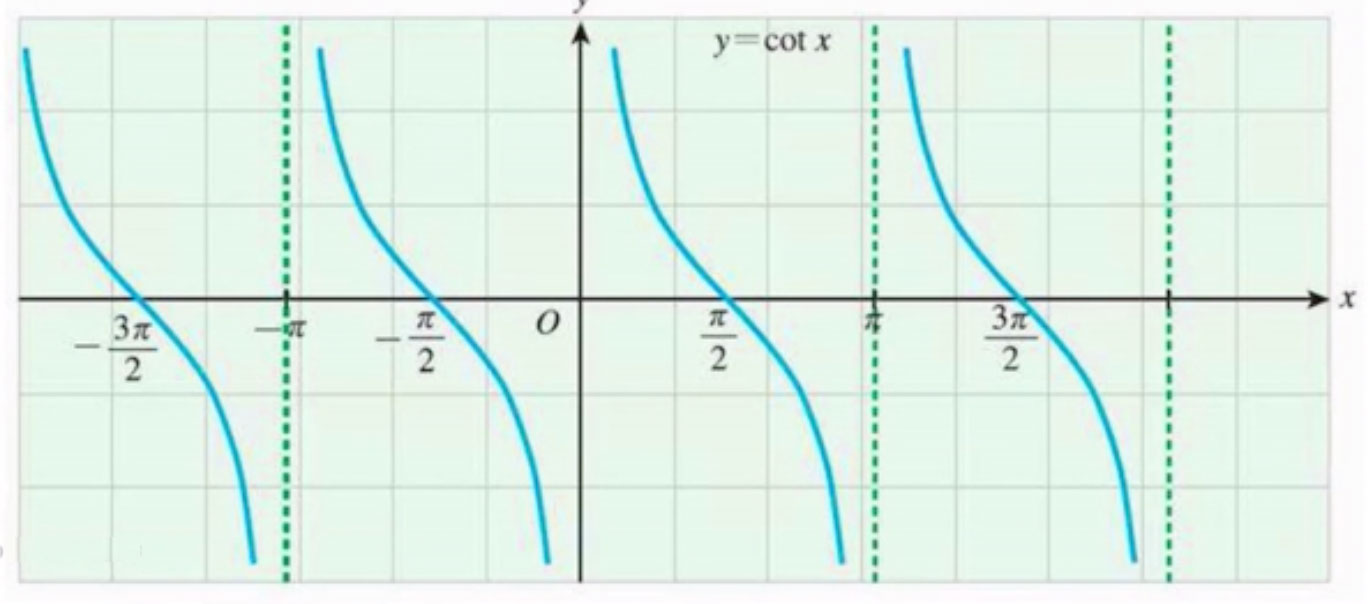
三角函数

正弦函数 y = sin x

余弦函数 y = cos x

正切函数 y = tan x

余切函数 y = cot x

机器学习中的应用

概念学习：从有关某个布尔函数的输入输出训练样例中推断出该布尔函数。
目标概念：Aldo 进行水止上运动的日子，表示为布尔函数 EnjoySport
任务目的：基于某天的各属性，预测 EnjoySport 的值
给定一个样例集 D：每个样例表示为6个属性的集合

概念学习

表3-1 目标概念 EnjoySport 的训练样例

Example	Sky	AirTemp	Humidity	Wind	Water	Forecast	EnjoySport
1	Sunny	Warm	Normal	Strong	Warm	Same	Yes
2	Sunny	Warm	High	Strong	Warm	Same	Yes
3	Rainy	Cold	High	Strong	Warm	Change	No
4	Rainy	Warm	High	Strong	Cool	Change	Yes

采取何种形式表示假设（目标函数的表示）
一个简单的形式，实例的各属性约束的合取式
令每个假设为6个约束（或变量）的向量，每个约束对应一个属性可取值范围，为
- ？任意本属性可接受的值
- 明确指定的属性值（如 AirTemp 中的 warm）
- ø不接受任何值

随堂例题

假设的例子

为判定 Aldo 只在寒冷和潮湿的日子进行水上运动：
<?,Cold,High,?,?,?>
最一般的假设是每一天都是正例，<?,?,?,?,?,?>
最特殊的假设是每一天都是反例，<ø,ø,ø,ø,ø,ø>

概念学习任务描述

实例的集合
实例集合上的目标函数
候选假设的集合
训练样例的集合

EnjoySport 概念学习任务

实例集 X：可能的日子，每个日子由下面的属性描述

Sky：可取值为 Sunny, Cloudy, Rainy
AirTemp：可取值为 Warm 和 Cold
Humidity：可取值为 Normal 和 High
Wind：可取值为 Strong 和 Weak
Water：可聚会为 Warm 和 Cool
Forecast：可取值为 Same 和 Change

目标概念

目标概念 c：待学习的目标概念或函数（target concept），记作 c，一般来说 c 可以是定义在实例集 X 上的任意布尔函数，即 c:X → {0,1}
此例为 EnjoySport：x → {0,1}
EnjoySport=Yes，c(x)=1
EnjoySport=No，c(x)=0

训练样例集合

训练样例集合 D：每个样例 X 中的一个实例 x 以及它的目标概念值 c(x)
目标函数的正例（positive example）：c(x) = 1
目标函数的反例（negative example）：c(x) = 0
描述训练样例的方式：序偶< x, c(x) >

假设集

假设集 H：每个假设描述为六个属性 Sky、AirTemp、Humidity、Wind、Water 和 Forecase的值约束的合取。
求解：H 中的一般假设 h，使得对于 X 中的任意 x，有 h(x) = c(x)

数列极限

数列与数列极限

割圆术

“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”

-刘徽

利用圆内接正多边形来推算圆面积的方法，是极限思想在几何学上的应用！

- 正六边形的面积 A₁
- 正十二边形的面积 A₂
  … …
- 正6×2^n-1形的面积 A_n

集合与运算

集合

集合概念的引入

集合的概念

集合相等

空集

集合的运算

并集

交集

差集

全集和补集

区间与邻域

区间

无限区间

邻域

机器学习中集合的应用

映射与函数

映射

映射的定义

映射三要素

注意

例题

函数的概念

函数的两要素

函数的图形表示方法

特殊函数举例

函数的特性

初等函数

机器学习中的应用

表3-1 目标概念 EnjoySport 的训练样例

随堂例题

数列极限

数列与数列极限

割圆术

截杖问题

收敛数列的性质

随堂练习

函数极限

函数极限概念

函数极限例题与单侧极限

函数极限的性质

章总结

随堂练习

无穷小与无穷大

无穷小

无穷大

章总结

随堂练习

极限运算

极限运算法则

极限运算法则（例题）

极限存在准则

无穷小的比较

章总结

随堂练习

函数的连续性与间断点

函数的连续性

函数的第一类间断点

函数的第二类间断点

章总结

随堂例题

导数与微分

导数的概念

导数的概念(幂函数求导-单侧导数-切线与法线方程)

函数的可导性与连续性

导数小结

函数的求导法则

复合函数的求导法则

常数和基本初等函数求导公式

高阶导数

高阶导数的运算法则

隐函数的导数

幂指函数求导

由参数方程确定的函数

函数的微分

微分运算法

微分中值定理与导数的应用

微分中值定理——罗尔定理

微分中值定理——拉格朗日中值定理

微分中值定理——柯西中值定理