生成式AI第三章 扩散模型Diffusion

图像生成领域在2014年因Ian Goodfellow引入生成对抗网络（GAN）而广泛流行。GAN的关键理念催生了一大批能够快速生成高质量图像的模型。然而，尽管GAN取得了成功，它也面临着挑战，需要大量参数并且难以有效泛化。这些限制引发了其它的研究尝试，带来了对扩散模型的探索——这是一类重新定义高质量、灵活图像生成的模型。

2020年底，一类鲜为人知的模型——扩散模型，开始在机器学习界引起轰动。研究人员发现如何使用这些扩散模型生成比GAN更高质量的图像。随后，出现了一系列的论文，提出了各种改进和修改，进一步提升了图像质量。到2021年底，像GLIDE这样的模型在文生图任务中展示了惊人的成果。仅几个月后，这些模型通过DALL-E 2和Stable Diffusion等工具进入了主流。普通人只需输入他们想看到的文字描述，就可以轻松生成图像。

在本章中，我们将深入探讨这些模型的工作原理。我们将综述使这些模型如此强大的关键思想，使用现有模型生成图像以了解其工作方式，然后训练我们自己的模型以进一步加深理解。该领域仍在快速发展，但这里涵盖的主题应该能为你提供一个坚实的基础，后续第5、7和8章将进一步扩展这些思想。

扩散模型的顶层思想是，接收带有噪声的模糊图像并学习去噪，输出清晰的图像。训练扩散模型时，数据集包含不同噪声程度的图像（输入可能是纯噪声）。在推理过程中，我们可以从纯噪声开始，模型将生成与训练分布相匹配的图像。模型通过多次迭代完成这一过程，不断自我纠正，最终生成令人惊叹的高质量图像。

本文相关代码请见GitHub仓库。

核心思想：迭代优化

那么，是什么使扩散模型如此强大呢？以前的技术，如变分自编码器（VAE）或GAN，通过模型的一次前向传递生成最终输出。这意味着模型必须在第一次尝试时就完全正确。如果出错，它不能回头修正。而扩散模型则通过多次迭代生成输出。这种迭代优化使模型能够纠正前几步中的错误，并逐步改进输出。为了说明这一点，我们来看一个扩散模型的实际例子。

我们可以使用Hugging Face的diffusers库加载一个预训练的扩散模型。该库提供了一个高阶管道，可以直接用于创建图像。我们将加载ddpm-celebahq-256模型，这是最早分享的高质量图像生成扩散模型之一。该模型使用CelebA-HQ数据集训练，这是一个包含高质量名人图像的流行数据集，因此它将生成看起来来自该数据集的图像。我们使用这个模型从噪声中生成图像。

该管道不会展示内部工作原理，下面深入了解其内部机制。如果运行代码，会注意到生成过程需要1000步。这条扩散管道必须经过1000次优化步骤（和前向传递）才能得到最终图像。这是与GAN相比，原始扩散模型的主要缺点之一——需要许多步才能生成高质量的图像，使得模型在推理时变得缓慢。

我们可以一步一步地重新创建这个采样过程，以更好地理解其底层机制。在扩散过程开始时，我们用四张随机图像初始化样本x（也即采样一些随机噪声）。我们将运行30步来逐步去噪输入图像，最终得到一个来自真实分布的样本。

一起生成一些图像吧！在左侧，可以看到给定步骤的输入（从随机噪声开始）。在右侧，可以看到模型对最终图像的预测。第一行的结果不是特别好。在给定的扩散步骤中，我们并不是直接跳到最终预测的图像，而是仅在预测方向上对输入x进行少量修改（如左侧所示）。然后，我们将这个新的、稍微改进的x再次输入模型进行下一步，希望得到一个略有改善的预测，用以进一步更新x，如此反复。经过足够多的步骤，模型可以生成一些非常逼真的图像。

注：如果代码看上去令人生畏，不用担心——我们将在本章中会讲解其原理。现在，重点关注概念思想。

这种逐步学习如何改进“有损”输入的核心思想可以应用于广泛的任务。本章将重点介绍无条件图像生成，生成类似于训练数据分布的图像。例如，我们可以用蝴蝶数据集训练一个无条件图像生成模型，这样它也能生成新的高质量图像。这个模型不能生成与其训练数据集分布不同的图像，所以不要期望它生成恐龙。在第4章中，我们将深入探讨基于文本条件的扩散模型，但我们还可以做很多其它方向。扩散模型已被应用于音频、视频、文本、3D物体、蛋白质结构等领域。虽然大多数实现使用我们将在这里介绍的某种去噪方法，但一些新兴的方法应用不同类型的“有损”（通常结合迭代优化），可能会使该领域超越当前对去噪扩散的关注。伟大的时代！

训练扩散模型

在本节中，我们将从头开始训练一个扩散模型，以更好地理解它们的工作原理。我们将使用diffusers库中的组件。随着本章的推进，我们将逐步揭开每个组件的神秘面纱。与其他生成模型相比，训练扩散模型相对简单。我们重复以下步骤训练模型：

1. 从训练数据中加载一些图像。
2. 添加不同程度的噪声。记住，我们希望模型能够很好地估计如何“修复”（去噪）噪声过大的图像和接近完美的图像，因此我们、、需要一个噪声多样化的数据集。
3. 将不同噪声输入版本喂给模型。
4. 评估模型在去噪的表现。
5. 使用该信息更新模型权重。

为用训练好的模型生成新图像，我们从一个完全随机的输入开始，并反复将其喂给模型，每次迭代根据模型预测对输入进行微量更新。我们会了解到有几种采样方法可以简化这一过程，以尽可能少的步骤生成良好的图像。

数据

本例中，我们将使用Hugging Face Hub上的一个图像数据集——具体来说，是一个包含1000张蝴蝶图片的数据集。稍后在项目部分，读者将了解到如何使用自己的数据。

在训练模型之前，我们必须准备数据。图像通常表现为一个像素网格，每个像素的三个颜色通道（红色、绿色和蓝色）具有0到255之间的颜色值。为处理这些图像并使其准备就绪待训练，我们需要：

• 将它们调整到固定大小。这是必要的，因为模型期望所有图像具有相同的尺寸。
• （可选）通过随机水平翻转图像来添加一些增强，这样可以使模型更加健壮，并获得更多数据进行训练。数据增强是计算机视觉任务中的常见做法，因为它有助于模型更好地泛化到未见过的数据。翻转只是图像数据增强的一种技术，其他技术包括平移、缩放和旋转。
• 将它们转换为PyTorch张量（颜色值表示为0到1之间的浮点数）。模型输入必须始终格式化为多维矩阵或张量。
• 规一化使其均值为0，值在-1到1之间。这是训练深度学习模型中的常见做法，因为它有助于模型更快更有效地学习。

我们可以使用torchvision.transforms定义这些转换：

注：torchvision是一个PyTorch库，提供大量处理图像的工具。本系列文章中我们仅使用此库做数据预处理迁移。

datasets库提供了便捷的方法set_transform()，可用于在使用数据时实时应用指定的转换。最后，可以使用加载工具DataLoader封装数据集使得对数据批次的迭代变容易，简化训练代码。

可以通过加载一个批次并审查图片来进行查看。

注：我们在本文中使用大于64×64的图像打印出美丽的蝴蝶，没有用像素化的图片。

这是我们在本章开始时用来说明迭代优化思想的相同代码，但此时更好地理解了所发生的事情。如若查看diffusers库中DDPMPipeline的实现，会发现其逻辑与我们上面的实现非常相似。

我们从一个完全随机的输入开始，然后模型在一系列步骤中对其进行优化。每一步都是在该时间步基于模型对噪声预测对输入进行的一次微更新。我们在调用pipeline.scheduler.step()时抽象掉了一些复杂性；稍后将深入探讨不同的采样方法及其工作原理。

添加噪声

如何逐渐破坏我们的数据？最常见的方法是向图像添加噪声。我们将向训练数据添加不同程度的噪声，因为我们的目标是训练一个无论输入中有多少噪声都能去噪的鲁棒模型。我们添加的噪声量由一个噪声调度控制。不同的论文和方法以不同的方式解决这个问题，我们将在本章后面进行探讨。现在，让我们看看基于DDPM论文的一种常见方法。在diffusers中，添加噪声是由一个名为Scheduler的对象处理的，该对象接受一批图像和一个时间步列表，并确定如何创建这些图像的噪声版本。我们将在本章后面探讨其背后的数学原理，但现在先看看它在实践中是如何工作的。

在训练过程中，我们会随机选择时间步。调度器接受一些参数（beta_start和beta_end），并使用这些参数来确定给定时间步的噪声量。我们将在后面的部分更详细地介绍调度器。

UNet

UNet是一种卷积神经网络，专为图像分割等任务而设计，其中所需的输出形状与输入相同。它由一系列下采样层组成，这些层减少了输入的空间大小，接着是一系列上采样层，这些层再次增加输入的空间范围。下采样层之后通常会有一个跳跃连接，将下采样层的输出连接到上采样层的输入。这允许上采样层“看到”网络此前的高分辨率表示，对于输出图像等任务来说是有益的，因为这些任务需要高分辨率信息。

diffusers库中使用的UNet架构比2015年提出的原始UNet更先进，增加了注意力和残差块等功能。我们稍后会更详细地研究，但这里的关键思想是它可以接收输入并生成与输入形状相同的预测。在扩散模型中，输入可以是一个有噪声的图像，而输出可以是预测的噪声。通过这些信息，我们现在可以对输入图像进行去噪。

下面是我们如何创建一个UNet并将一批有噪声的图像输入其中的方法：

from torch.nn import functional as F num_epochs = 50 # How many runs through the data should we do? lr = 1e-4 # What learning rate should we use optimizer = torch.optim.AdamW(model.parameters(), lr=lr) losses = [] # Somewhere to store the loss values for later plotting # Train the model (this takes a while!) for epoch in range(num_epochs): for batch in train_dataloader: # Load the input images clean_images = batch["images"].to(device) # Sample noise to add to the images noise = torch.randn(clean_images.shape).to(device) # Sample a random timestep for each image timesteps = torch.randint( 0, scheduler.config.num_train_timesteps, (clean_images.shape[0],), device=device, ).long() # Add noise to the clean images according # to the noise magnitude at each timestep noisy_images = scheduler.add_noise(clean_images, noise, timesteps) # Get the model prediction for the noise # The model also uses the timestep as an input # for additional conditioning noise_pred = model(noisy_images, timesteps, return_dict=False)[0] # Compare the prediction with the actual noise loss = F.mse_loss(noise_pred, noise) # Store the loss for later plotting losses.append(loss.item()) # Update the model parameters with the optimizer based on this loss loss.backward(loss) optimizer.step() optimizer.zero_grad()

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

from torch.nn import functional as F   num_epochs = 50  # How many runs through the data should we do? lr = 1e-4  # What learning rate should we use optimizer = torch.optim.AdamW(model.parameters(), lr=lr) losses = []  # Somewhere to store the loss values for later plotting   # Train the model (this takes a while!) for epoch in range(num_epochs):     for batch in train_dataloader:         # Load the input images         clean_images = batch["images"].to(device)           # Sample noise to add to the images         noise = torch.randn(clean_images.shape).to(device)           # Sample a random timestep for each image         timesteps = torch.randint(             0,             scheduler.config.num_train_timesteps,             (clean_images.shape[0],),             device=device,         ).long()           # Add noise to the clean images according         # to the noise magnitude at each timestep         noisy_images = scheduler.add_noise(clean_images, noise, timesteps)           # Get the model prediction for the noise         # The model also uses the timestep as an input         # for additional conditioning         noise_pred = model(noisy_images, timesteps, return_dict=False)[0]           # Compare the prediction with the actual noise         loss = F.mse_loss(noise_pred, noise)           # Store the loss for later plotting         losses.append(loss.item())           # Update the model parameters with the optimizer based on this loss         loss.backward(loss)         optimizer.step()         optimizer.zero_grad()

from matplotlib import pyplot as plt plt.subplots(1, 2, figsize=(12, 4)) plt.subplot(1, 2, 1) plt.plot(losses) plt.title("Training loss") plt.xlabel("Training step") plt.subplot(1, 2, 2) plt.plot(range(400, len(losses)), losses[400:]) plt.title("Training loss from step 400") plt.xlabel("Training step")

1 2 3 4 5 6 7 8 9 10 11 12 13

from matplotlib import pyplot as plt   plt.subplots(1, 2, figsize=(12, 4))   plt.subplot(1, 2, 1) plt.plot(losses) plt.title("Training loss") plt.xlabel("Training step")   plt.subplot(1, 2, 2) plt.plot(range(400, len(losses)), losses[400:]) plt.title("Training loss from step 400") plt.xlabel("Training step")

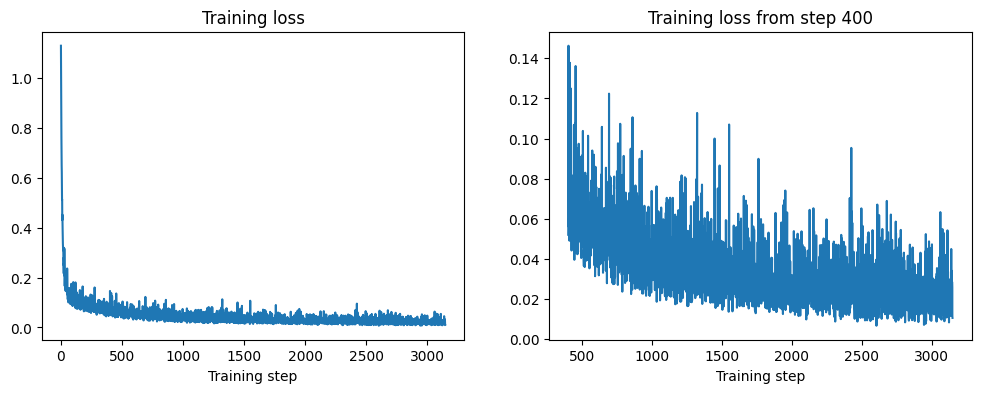
损失曲线随着模型学习去噪图像而呈下降趋势。曲线有些噪声——损失不太稳定。这是因为每次迭代使用的加噪时间步数不同。通过观察噪声预测的均方误差，很难判断这个模型在生成样本方面的表现如何，所以进入下一节，看看它的实际效果。

采样

现在有了一个模型，让我们进行推理并生成一些图像。diffusers库使用管道的概念将生成扩散模型样本所需的所有组件打包在一起：

注：模型所生成的图像是以64×64分辨率训练并放大，所以看起来有些像素化。

pipeline = DDPMPipeline(unet=model, scheduler=scheduler) ims = pipeline(batch_size=4).images show_images(ims, nrows=1)

1 2 3

pipeline = DDPMPipeline(unet=model, scheduler=scheduler) ims = pipeline(batch_size=4).images show_images(ims, nrows=1)

0%| | 0/1000 [00:00<?, ?it/s]

1	0%|          | 0/1000 [00:00<?, ?it/s]

将创建样本的任务交给管道处理不会让我们看到内部的工作原理。因此，下面进行一个简单的采样循环，展示模型如何根据管道的call() 方法中的代码逐步优化输入图像。

# Random starting point (4 random images): sample = torch.randn(4, 3, 64, 64).to(device) for t in scheduler.timesteps: # Get the model prediction with torch.no_grad(): noise_pred = model(sample, t)["sample"] # Update sample with step sample = scheduler.step(noise_pred, t, sample).prev_sample show_images(sample.clip(-1, 1) * 0.5 + 0.5, nrows=1)

1 2 3 4 5 6 7 8 9 10 11 12

# Random starting point (4 random images): sample = torch.randn(4, 3, 64, 64).to(device)   for t in scheduler.timesteps:     # Get the model prediction     with torch.no_grad():         noise_pred = model(sample, t)["sample"]       # Update sample with step     sample = scheduler.step(noise_pred, t, sample).prev_sample   show_images(sample.clip(-1, 1) * 0.5 + 0.5, nrows=1)

这与我们在本章开头用来说明迭代优化思想的代码相同，但现在更清楚这里发生了什么。如果你查看diffusers库中DDPMPipeline的实现，会发现其逻辑与我们上面的实现非常相似。

我们从一个完全随机的输入开始，然后模型通过一系列步骤进行优化。每一步都是基于模型对该时间步噪声的预测，对输入进行的小更新。我们仍然将一些复杂性抽象在ipeline.scheduler.step()的调用背后；稍后，我们将深入探讨不同的采样方法及其工作原理。

评估

评估生成模型是复杂的——它本质上是一项主观任务。例如，给定一个输入提示词“image of a cat with sunglasses”，可能有许多正确的生成结果。一种常见的方法是结合定性评估（例如，通过让人类比较生成结果）和定量指标，这些指标提供了评估框架，但不一定对应于高图像质量。

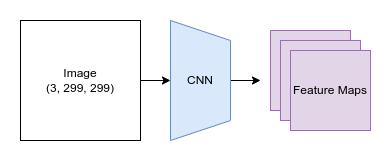
FID分数（Fréchet Inception Distance）可以用来评估生成模型的性能。FID分数比较两个图像数据集的相似度。它们使用预训练的神经网络，通过比较从两个数据集中提取的特征图之间的统计数据，来衡量生成样本与真实样本的匹配程度。分数越低，给定模型生成的图像质量和真实感越好。由于FID分数能够为不同类型的生成网络提供“客观”的比较指标，而不依赖于人工判断，因此它们非常受欢迎。

示例 3-1. CNN提取特征图的图示

尽管FID打分非常方便，但有一些重要的注意事项（这对于其他评估指标也可能适用）：

• FID分数设计用于比较两个分布。因此，它假定我们可以访问用于比较的源数据集。第二个问题是，无法计算出单个生成图像的FID分数。如果只有一张图像，就无法计算其FID分数。
• 给定模型的FID分数取决于用于计算的样本数量，因此在比较模型时，我们需要确保两个报告的分数都使用相同数量的样本计算。常见的做法是使用50,000个样本，但为节省时间，可以在开发过程中评估较少数量的样本，并且只在准备发布结果时进行完整评估。
• FID对许多因素都很敏感。例如，不同数量的推理步骤将产生截然不同的FID分数。调度器（在本例中为DDPM）也会影响FID。
• 计算FID时，图像会被调整为299像素的方形图像。这使得它作为极低或极高分辨率图像的指标时实用性较低。不同深度学习框架在处理图像调整时也会有细微差异，可能导致FID分数的轻微差异。
• 用于FID的特征提取网络通常是一个在ImageNet分类任务上训练的模型。在生成不同领域的图像时，该模型学习的特征可能不那么有用。更准确的方法是首先在特定领域数据上训练一个分类网络，这使得不同论文和技术之间的分数比较更加困难。目前，ImageNet模型是标准选择。
  注：ImageNet是计算机视觉最知名的基准之一。它包含几千个分类数百万张图片，这使其成为训练和基准测试基础模型的知名数据集。
• 如果保存生成的样本供后续评估，格式和压缩方式可能会再次影响FID分数。尽量避免使用低质量的JPEG图像。

即使考虑到所有这些注意事项，FID分数也只是质量的粗略衡量标准，并不能完美捕捉使图像看起来更“真实”的细微差别。生成模型的评估是一个活跃的研究领域。标准指标如Kernel Inception Distance（KID）和Inception Score与FID存在类似的问题。因此，使用这些指标可以了解一个模型相对于另一个模型的性能，但也要查看每个模型生成的实际图像，以更好地比较它们。人类偏好仍然是最终的质量标准，这毕竟是一个相当主观的领域。例如，Parti Prompts数据集包含1600个不同难度和类别的提示词，允许比较我们将在第4章探索的文生图模型。

注：要深入了解评估扩散模型的知识，建议查阅diffusers库的评估扩散模型文档。

深入：噪声调度

在上面的训练示例中，其中一个步骤是“添加不同量的噪声”。我们通过在0到1000之间选择一个随机时间步，然后依赖调度器添加适量的噪声来实现这一点。同样，在推理过程中，我们再次依赖调度器告诉我们使用哪些时间步以及如何根据模型预测从一个时间步移动到下一个。选择添加多少噪声是一个关键的设计决策，它可以极大地影响给定模型的性能。在本节中，我们将了解为什么是这样，并探究实践中使用的不同方法。

为什么要添加噪声？

在本章开始时，我们说过扩散模型背后的关键思想是迭代优化。在训练过程中，我们以不同程度破坏输入。在推理过程中，我们从一个最大程度损坏的输入开始（即纯噪声图像），并不断地去噪，期望最终得到一个良好的结果。

到目前为止，我们关注的是一种特定类型的破坏：添加高斯噪声。高斯噪声是一种遵循正态分布的噪声，这意味着它有一个钟形曲线，大多数值聚集在均值周围，极值较少（通过torch.rand_like()添加高斯模糊）。我们关注这种噪声的一个原因是扩散模型的理论基础，它假设使用高斯噪声——如果我们使用不同的损坏方法，技术上就不再是扩散。然而，一篇名为《冷扩散》的论文表明，为了理论上的便利，我们不必限定在这种方法上。他们展示了扩散模型类似的方法对许多不同的损坏方法都有效。这意味着我们可以使用其他图像变换替代噪声。例如，Muse、MaskGIT和Paella等模型使用随机标记屏蔽或替换作为等效的破坏方法。

尽管如此，添加噪声仍然是最流行的方法，原因有：

• 我们可以轻松控制添加的噪声量，从“完美”到“完全损坏”之间平滑过渡。对于像降低图像分辨率这类任务，情况并非如此，这可能导致“离散”的过渡。
• 我们可以为推理提供许多有效的随机起点，不像一些方法，可能只有有限数量的初始（完全损坏）状态，例如完全黑色的图像或单像素图像。

因此，现在我们将添加噪声作为我们的破坏方法。接下来，我们来看如何向图像添加噪声。

从简单处开始

我们有一些图像x，并希望向它们添加一些随机噪声。使用torch.rand_like()生成与输入图像尺寸相同的纯高斯噪声。

我们可以通过在图像和噪声之间按一定量的线性插值（简称“lerp”）来添加不同量的噪声。这为我们提供了一个函数，当amount从0变化到1时，该函数从原始图像x平滑过渡到纯噪声：

我们对一批数据进行实践，噪声量从0到1不等：

这实现了从原始图像平滑过渡到纯噪声的目标。我们使用连续时间方法创建了一个噪声调度，其中将整个路径表示为从0到1的时间刻度。其他方法使用离散时间方法，使用一些大的整数时间步来定义噪声调度器。可以将函数封装到一个类中，该类将连续时间转换为离散时间步并适当地添加噪声：

现在我们有了可以直接与diffusers库中使用的调度器（例如我们在训练期间使用的DDPMScheduler）进行比较的参照。下面看看它们的比较结果：

可以看到，虽然不完全相同，但足以供我们探索使用噪声调度器进行模型训练。

数学原理

我们来深入讲解一下将噪声添加到原始图像的数学原理。需要注意，文献中有许多符号和方法。例如，在一些论文中，噪声调度是连续参数化的，因此t从0（无噪声）到1（完全破坏），就像在corrupt函数中那样。其他论文使用离散时间方法，其中时间步是整数，从0到某个大数T，通常为1000。可以像在SimpleScheduler类中那样在这两种方法之间进行转换——在比较不同模型时确保一致性非常重要。这里我们将保持使用离散时间方法。

深入数学原理的一个不错的起点是DDPM论文或带注解的实现。如果读者觉得这部分内容过于复杂，可以先专注于上层的概念，稍后再回来看数学部分。

注：带注解的实现是一篇优秀的博文，从头讲解并实现了整个扩散处理。

让我们开始定义如何处理从时间步t-1到时间步t的单次增噪步骤。前文提到，理念是添加高斯噪声($\epsilon$).。这种噪声具有单位方差，控制噪声值的分布。通过将噪声添加到前一步的图像中，我们逐渐破坏原始图像，这是扩散模型训练过程的关键部分。

$$x_t = x_{t-1} + \epsilon$$

为控制每一步添加的噪声量，我们引入参数$\beta_t$。该参数定义于所有时间步t上，指定每一步应该添加多少噪声。换句话说，$x_t$是$x_{t-1}$和一些按$\beta_t$缩放的随机噪声的融合。这使得我们能够在通过时间步移动时逐渐增加添加到图像中的噪声量，这是扩散模型训练过程的关键部分。

$$x_t = \sqrt{1 – \beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon$$

我们可以进一步将噪声添加过程定义为一个分布，其中带噪声的$x_t$均值为$\sqrt{1 – \beta_t}x_{t-1}$，方差为$\beta_t$。这个分布帮助我们更准确地建模增噪过程。下面是分布形式的公式：

$$q(x_t|x_{t-1}) = \mathcal{N}(x_t;\sqrt{1 – \beta_t}x_{t-1},\beta_tI)$$

注：在统计学中，分布是一种描述变量值如何展开的方式。展示不同变量值出现的频率。

现在已经定义了一个分布，以便在前一个值的条件下采样x。为在时间步t获得带噪声的输入，我们可以从t=0开始，反复应用这个单步过程，这样很低效。而我们可以通过重新参数化的技巧找到一个公式来一次移动到任意时间步t。思想是预计算噪声调度，由$\beta_t$值定义。然后可以定义$\alpha_t = 1 – \beta_t$以及$\bar{\alpha}$作为时间步t所有$\alpha$的累计乘积，可以表示为$\bar{\alpha} := \prod_{s=1}^t\alpha_s$。使用这些工具和符号，我们可以重新定义分布及如何在特定时间采样。新的分布$q(x_t|x_{t-1})$具有均值$\bar{\alpha_t}x_{t-1}$和方差$(1-\bar{\alpha_t})I$。

$$q(x_t|x_{t-1}) = \mathcal{N}(x_t;\bar{\alpha_t}x_{t-1}, (1-\bar{\alpha_t})I).$$

探索这个重新参数化的技巧是本章末挑战的一部分。现在可以使用以下公式在时间步t采样带噪声的图像：

$$x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 – \bar{\alpha}_t}\epsilon$$

公式中的$x_t$表明时间步t的带噪声输入是原始图像$x_0$（以$\sqrt{\bar{a}_t}$缩放）和噪声$\epsilon$（以$\sqrt{1 – \bar{\alpha}_t}$缩放）的组合。请注意，我们现在可以直接计算采样，而不需要循环所有前面的时间步，这使得训练扩散模型更加高效。

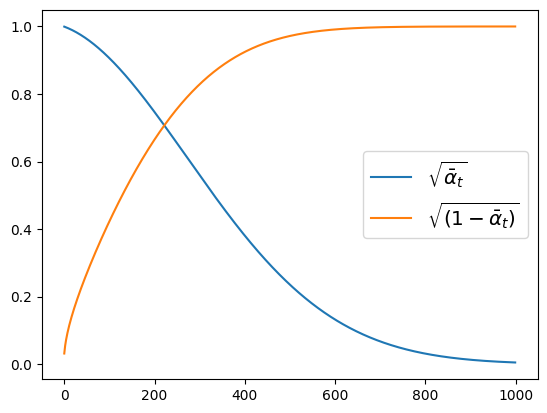
在diffusers库中，$\bar{\alpha}$值存储于scheduler.alphas_cumprod中。知道这一点后，我们可以绘制原始图像$x_0$和噪声ε在给定调度器的不同时间步中的缩放因子。diffusers库允许我们通过定义初始值（beta_start）、最终值（beta_end）和步长（例如线性（beta_schedule="linear"））来控制β值。下图显示了随着时间步的增加，噪声的缩放量增加，这和预想一致。

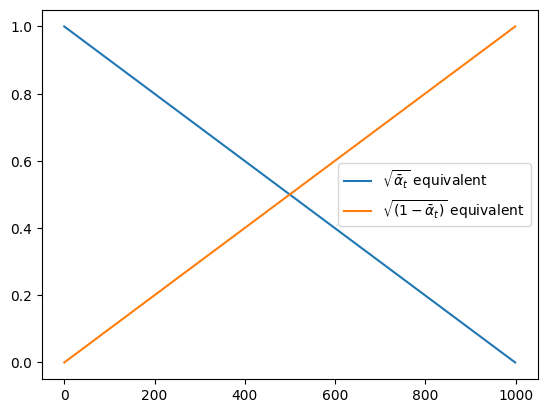
我们的SimpleScheduler只是将原始图像和噪声进行了线性融合，通过绘制缩放因子可以看出（相当于DDPM案例中的$\sqrt{\bar{a}_t}$和$\sqrt{1 – \bar{\alpha}_t}$）：

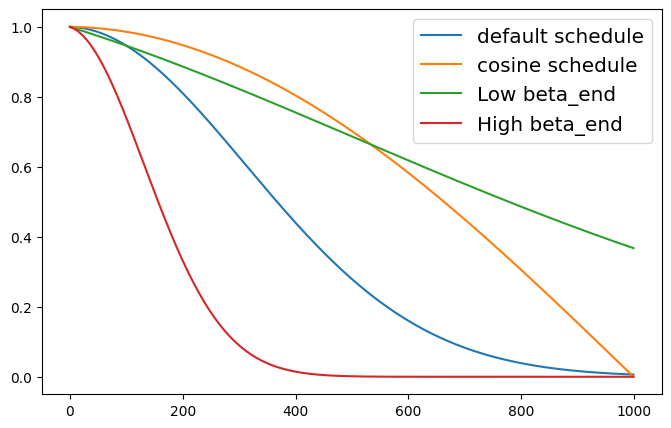
好的噪声调度会确保模型在不同噪声级别下看到融合的图像。最佳选择将取决于训练数据。可视化更多选项时，要注意：

• 将 beta_end 设置得太低意味着我们从未完全破坏图像，因此模型将永远不会看到任何类似于用于推理起点的随机噪声。
• 将 beta_end 设置得过高意味着大多数时间步都花在几乎完全的噪声上，从而导致训练性能不佳。
• 不同的 beta 调度会产生不同的曲线。余弦调度很受欢迎，因为它可以平滑地从原始图像过渡到噪声。

下面来做可视化。

注：这里展示的所有调度都称为方差保持（VP），这意味着模型输入的方差在整个调度过程中保持接近1。还可能遇到方差爆炸（VE）公式，其中噪声以不同的量添加到原始图像中（导致高方差输入）。我们的 SimpleScheduler 几乎是一个 VP 计划，但由于线性插值，方差并未能完全保持。

与许多扩散相关的话题一样，不断有新论文探讨噪声调度，因此在读者阅读本文时，可能已经有大量选项可以尝试。

输入分辨率和缩放的影响

直到最近，噪声计划的一个方面——输入大小和缩放的影响——大多被忽视了。许多论文在小规模数据集和低分辨率下测试潜在的调度器，然后使用表现最好的调度器在更大图像上训练最终模型。如果我们向两张不同大小的图像添加相同量的噪声，可以看出这个问题：

高分辨率图像往往包含大量冗余信息。这意味着即使单个像素被噪声遮蔽，周围像素也有足够的信息来重建原始图像。对于低分辨率图像则不同，其中单个像素可以包含大量有用信息。向低分辨率图像添加相同量的噪声将导致比向高分辨率图像添加等量噪声更严重的图像损坏。

2023年初的两篇论文详细研究了这一效应。每篇论文都利用新见解训练出能够生成高分辨率输出的模型，而无需以前所需的任何技巧。Simple diffusion引入了一种根据输入大小调整噪声调度的方法，使得在低分辨率图像上优化的计划可以适当地调整为新的目标分辨率。另一篇论文进行了类似的实验，并指出了另一个关键变量：输入缩放。也就是说，如何表示我们的图像？如果图像表示为0到1之间的浮点数，它们的方差将低于噪声（通常是单位方差）。因此，对于给定的噪声水平，信噪比将低于图像表示为-1到1之间的浮点数（我们在上面的训练示例中使用的就是-1到1）或其他表示方式。缩放输入图像会改变信噪比，因此修改这一缩放是训练大图像时做调整的另一种方法。

深入分析：UNet 和替代方案

我们来讨论一下做出关键预测的实际模型。回顾一下，这个模型必须能够接收一个有噪声的图像并输出其噪声，从而使输入图像去噪。这需要一个能够接收任意大小图像并输出相同大小图像的模型。此外，该模型应能够在像素级别进行精确预测，同时捕捉图像的高层次信息。一种流行的方法是使用称为 UNet 的架构。UNet 于2015年为医学图像识别而发明，自此成为各种图像相关任务的热门选择。

与我们在上一章中看到的自动编码器和 VAE 类似，UNet 由一系列下采样和上采样块组成。下采样块负责减小图像大小，而上采样块负责增加图像尺寸。下采样块通常由一系列卷积层、一个池化或下采样层组成。上采样块通常包括一系列卷积层，后接一个上采样或转置卷积层。转置卷积层是一种特殊类型的卷积层，它增加图像的大小而不是减小图像的大小。

常规自动编码器和 VAE 不是这个任务的好选择，因为它们在像素级别进行精确预测的能力较差，必须从低维潜在空间重建图像。在 UNet 中，下采样块和上采样块通过跳跃连接相连，让信息直接从下采样块流向上采样块。这使得模型能够在像素级别进行精确预测，同时捕捉图像整体的顶层信息。

一个简单的 UNet

为了更好地理解 UNet 的结构，我们从头开始构建一个简单的 UNet。

图3-1：UNet

我们将设计一个适用于单通道图像（例如灰度图像）的 UNet，可以用它来构建用于数据集（如 MNIST）的扩散模型。我们将在下采样路径中使用三层，在上采样路径中使用另三层。每一层由一个卷积层、一个激活函数以及一个上采样或下采样步骤组成，具体取决于它们是在编码路径还是解码路径中。如前所述，跳跃连接直接将下采样块连接到上采样块。实现跳跃连接的方法有多种。

我们将在这里使用的一种方法是将下采样块的输出添加到相应上采样块的输入。另一种方法是将下采样块的输出与上采样块的输入连接起来。甚至可以在跳跃连接中添加一些额外的层。现在，我们用最初的方法以保持简单。以下是这个网络的代码：

如果输入一个形状为 (1, 28, 28) 的灰度图像，通过模型的路径如下：

1. 图像首先通过下采样块。第一层是具有32个滤波器的2D卷积层，将其变为形状 [32, 28, 28]。
2. 然后图像通过最大池化进行下采样，变为形状 [32, 14, 14]。MNIST 数据集包含在黑色背景（黑色用数字零表示）上绘制的白色数字。我们选择最大池化来选择区域内的最大值，从而关注最亮的像素。
   注：出于可视化目的，我们将MNIST数据集显示为白色背景上的黑色数字，但训练数据集恰恰相反。
3. 图像接着通过第二个下采样块。第二层是具有64个滤波器的2D卷积层，将其变为形状 [64, 14, 14]。
4. 经过另一轮下采样后，形状变为 [64, 7, 7]。
5. 在下采样块中有第三层，但这次不进行下采样，因为我们已经在使用非常小的 7x7 块。这将保持形状为 [64, 7, 7]。
6. 我们以相同的流程反向上采样，分别变为 [64, 14, 14]、[32, 14, 14]，最后是 [1, 28, 28]。

使用这种架构在 MNIST 上训练的扩散模型生成了以下样本（代码在补充材料中，为简洁起见在此省略）：

图3-2：基础UNet的损失和生成

图3-3： 高级UNet的损失和生成

替代架构

最近提出了几种用于扩散模型的替代架构。包括：

• Transformer。Diffusion Transformers 论文展示了一种基于 transformer 的架构可以训练出性能优异的扩散模型。然而，transformer 架构的算力和内存需求在处理非常高分辨率时仍然是一个挑战。
• UViT。Simple Diffusion 论文中的 UViT 架构通过用大量的 transformer 块替换 UNet 的中间层，旨在两全其美。该论文的一个关键见解是，将大部分计算集中在 UNet 的低分辨率块上，可以更有效地训练高分辨率扩散模型。对于非常高的分辨率，通过使用一种称为小波变换的预处理方法来减少输入图像的空间分辨率，同时通过增加通道数尽可能保留信息，从而减少在较高空间分辨率上所需的计算量。
• 循环接口网络（Recurrent Interface Networks）。RIN 论文采取了类似的方法，首先将高分辨率输入映射到更易管理的低维潜在表示，然后通过一堆 Transformer 块处理，再解码回图像。此外，RIN 论文引入了递归的概念，即从上一个处理步骤向模型传递信息。这可以有助于扩散模型设计的迭代改进。

目前尚不清楚基于 transformer 的方法是否会完全取代 UNet 作为扩散模型的首选架构，或者像 UViT 和 RIN 这样的混合方法是否会最有效。

深入分析：目标和预处理

我们已经讨论了扩散模型接受噪声输入并学习去噪。乍一看，你可能认为网络的自然预测目标是图像的去噪版本，我们称之为 x0。然而，我们在代码中将模型预测与用于创建噪声版本的单位方差噪声（通常称为 epsilon 目标，eps）进行了比较。这两者在数学上看起来是相同的，因为如果我们知道噪声和时间步长，我们可以推导出 x0，反之亦然。虽然是这样，但目标的选择对不同时间步长的损失大小以及模型最擅长去噪的噪声水平有一些微妙的影响。预测噪声对模型来说比直接预测目标数据更容易。这是因为每一步的噪声遵循已知的分布，预测两步之间的差异通常比预测目标数据的绝对值更简单。

为了获得一些直观的认识，让我们可视化不同时间步长的不同目标。输入图像和随机噪声是相同的（示意图中的前两行），但第三行的噪声图像根据时间步长添加了不同量的噪声。

在极低噪声水平下，x0 目标极其简单（噪声图像与输入几乎相同），准确预测噪声几乎是不可能的。同样地，在极高噪声水平下，eps 目标很直接（噪声图像几乎等于添加的纯噪声），准确预测去噪图像几乎是不可能的。如果我们使用 x0 目标，训练时会对较低噪声水平赋予较小的权重。这两种情况都不理想，因此引入了额外的目标，让模型在不同时间步长上预测 x0 和 eps 的混合体。速度 (v) 目标是其中一种目标，定义为 $v = \sqrt{\alpha_t} x_0 – \sqrt{1 – \alpha_t} \epsilon $。eps 目标仍然是最受欢迎的方法之一，但了解其缺点和其他目标的存在是很重要的。

注：NVIDIA 的一个研究团队致力于将不同的扩散模型公式统一到一个一致的框架中，并明确区分设计选择。这使他们能够识别采样和训练过程中的变化，从而提高性能，形成了所谓的 k-diffusion。如果你对了解不同目标、缩放以及扩散模型公式的细微差别感兴趣，推荐阅读 EDM 论文以获取更深入的讨论 。

项目实战：训练自己的扩散模型

好了，理论讲得够多了。现在是时候训练自己的无条件扩散模型了。和之前一样，我们将训练一个模型来生成新图像。本项目的主要挑战是创建或找到一个可以使用的好数据集。

如果想使用现有的数据集，可以过滤 Hugging Face Hub 上的图像分类数据集开始，选择一个你喜欢的。需要回答的主要问题之一是你想用数据集的哪一部分进行训练。是像之前一样使用整个数据集，让模型生成数字吗？还是会使用特定的类别，例如猫，从而得到一个猫专家模型？还是会使用数据集的一个子集，例如只包含某个分辨率的图像？

如果想上传一个新数据集，第一步是找到并访问数据。分享数据集最简单的方法是使用 datasets 库的 ImageFolder 功能。然后可以将数据集上传到 Hugging Face Hub 并在项目中使用。

一旦有了数据，思考预处理步骤、模型定义和训练循环。可以先使用本章的代码，并根据数据集进行修改。

总结

我们从使用高级管道来进行扩散模型推理开始，最终从头训练我们的扩散模型并深入了解每个组件。下面简要回顾一下。

目标是训练一个通常是 UNet 的模型，接收噪声图像作为输入，并能预测该图像的噪声部分。在训练模型时，我们根据随机的时间步长添加不同程度的噪声。我们看到的一个挑战是，如果要在大量步骤（例如 900 步）中添加噪声，需要进行大量的噪声迭代。为解决这个问题，我们使用重新参数化技巧，这使我们能够直接在特定时间步长上获得噪声输入。模型被训练以最小化噪声预测与实际输入噪声之间的差异。在推理过程中，我们进行迭代细化过程，模型细化初始随机输入。我们不是保留单个扩散步骤的最终预测，而是通过小幅度调整输入 x 向该预测方向进行迭代修改。当然，这也是扩散模型推理往往较慢的原因之一，与 GAN 等模型相比，这是其主要缺点之一。

这个过程涉及许多动态部分，因此解释概念以确保能理解非常重要。扩散领域发展迅速，有许多进展（例如调度器、模型、训练技术等）。本章侧重于基础知识，使我们能够跳到条件生成（例如，生成受输入提示条件影响的图像），并为深入扩散领域提供背景。本章中的一些阅读材料可以帮助你深入了解。

推荐阅读：

• The Annotated Diffusion Model：这篇博客对 DDPM 论文进行了技术性讲解。访问地址：https://huggingface.co/blog/annotated-diffusion
• Lilian Weng 的文章非常适合深入了解数学。访问地址：https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
• Denoising Diffusion Probabilistic Models 论文。
• Karras 关于统一扩散模型公式的工作。
• Simple Diffusion，解释如何调整不同大小的样本调度。

练习

1. 解释扩散推理算法。
2. 噪声调度器的作用是什么？
3. 在创建图像训练数据集时，有哪些重要特性？
4. 为什么我们随机翻转训练图像？
5. 我们如何评估扩散模型的生成效果？
6. beta_end 的值如何影响扩散过程？
7. 我们为什么使用 UNet 而不是 VAE 作为扩散的主要模型？
8. 在将 transformer 技术（如注意力层或基于 transformer 的架构）引入扩散模型时，面临哪些好处和挑战？
   挑战
9. 证明 $$x_t = \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon$$
   等价于$$x_t = \sqrt{\bar{a_t}} x_{0} + \sqrt{1-\bar{a_t}} \epsilon$$
   注意这不是一个简单的示例，也不是使用扩散模型所必需的。建议精读或参考《A Beginner’s Guide to Diffusion Models: Understanding the Basics and Beyond》。一个重要的知识点是了解如何合并两个高斯：如果有两个方差不同的高斯$\mathcal{N}(\mu_1,\sigma_1^2)$和$\mathcal{N}(\mu_2,\sigma_2^2)$，结果高斯是 $\mathcal{N}(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$。
10. 本章使用了 DDPM 调度器，有时需要数百或数千步才能得到高质量的结果。最近的研究探索了如何在尽可能少的步骤下实现良好的生成，甚至少至一两步！diffusers 库包含多个调度器，例如 Denoising Diffusion Implicit Models 论文中的 DDIMScheduler 。使用 DDIMScheduler 创建一些图像。本章的采样部分使用 DDPMScheduler 需要 1000 步。需要多少步才能生成质量相似的图像？尝试切换调度器为 google/ddpm-celebahq-256 并比较两个调度器。

喜欢 (0)赏

[]

分享 (0)