第一章 成为一个随机应变的思考者

本文为Python之 AI人工智能初学者指南第一章。

2017年5月，Google 发布了AutoML，一个自动化机器学习系统，无需人类工程师的协助即可创建人工智能解决方案。IBM云和亚马逊云服务（AWS）提供了无需AI开发人员的机器学习方案。GitHub和其它云平台提供了几千个机器学习项目，降低了对于随身有AI专家的需求。这些云平台将慢慢地也必然会减少对于人工智能开发人员的需求。Google云的AI提供了符合人类习惯的机器学习服务。Microsoft Azure提供了用户友好的机器学习界面。

同时，大型开放式在线教育（MOOC-Massive Open Online Courses）则遍地开花。任何人可以在任意地方拿着GitHub上的机器学习方案，透过MOOC而无需进入大学学习，就有机会打败在岗的工程师。

如今，人工智能更多的是将数学转译为源代码，这让传统的开人员学习起来非常困难。这是也为什么Google, IBM, Amazon, Microsoft和其它公司开放预置的云端解决方案来在将来减少对工程师的需求。

读者会看到，从本章开始，你可以作为一个随机应变的思考者来占据这个世界的 C 位。没有时间可以浪费了。本章中，我们将快速直接地深入到强化学习中，这是Google Alphabet的DeepMind项目的其中一个核心基石（另一个是神经网络）。强化学习经常使用马尔科夫决策过程（Markov Decision Process (MDP)）。MDP包含带有学习参数的无记忆和无标签的动作回报方程式。这一方程，贝尔曼方程（常被称为Q函数）用于打败世界级的Atari游戏玩家。

这里的目标不是简单地走捷径。我们致力于将复杂内容分解为易于理解的部分并与现实世界相结合。读取者会从头学习如何应用随机应变思考者的过程，来在增强学习中将想法转变为解决方案，也会深入到Google的DeepMind项目重心之中。

本章讲解的内容有：

• 实现AI, ML和DL的三维方法
• 强化学习
• MDP
• 无监督学习
• 随机（Stochastic）学习
• 无记忆（Memoryless）学习
• 贝尔曼方程
• 收敛(Convergence)
• 使用Q动作值（action-value）函数的强化学习Python示例
• 在快递示例中应用强化学习

技术准备

• Python 3.6x 64位（官网：https://www.python.org/）
• Python 3.6x的NumPy
• Github上的程序Chapter01 MDP.py

访问如下视频来查看实时的代码操作：

如何成为随机应变的思考者

强化学习是机器学习一个基础，通过与环境交互的尝试与错误中进行学习。这听起来很熟悉，不是吗？这是正是我们人类一生都在做的事-有些痛苦！尝试事物、评估然后继续，或者尝试其它事物。

在现实生活中，你是你自己思考进程的代理。在机器学习模型中，代理是通过这一试错进程计算的函数。机器学习中的这一思考进程就是MDP。这种动作值形式的学习有时被称为Q。

要掌握理论和实践中MDP的结果，先决条件是三维方法。

三维方法会让你成为一个人工智能卖家，总而言之它表示：

• 使用现实生活的用例描述待解决的问题
• 然后建立数学模型
• 再后，编写源代码并且/或者使用一个云平台解决方案

这是你从一开始以随机应变姿态进入任何项目的一种方法。

在编写方案前解决现实生活问题

本章中，我们将来处理马尔科夫决策过程（Q函数）并使用贝尔曼方程将其应用于强化学习。读者可以在网上找到无数的源代码的示例。但是，大多数都是与现实生活无关的玩具实验。例如，强化学习可应用于电商行的快递员、自动驾驶或无人机。我们会看一个计算无人机快递的程序。但是，需要克服很多限制。作为一个随机应变的思考者的你会问这些问题：

• 如果在一个大城市中同时有5,000个无人机怎么办？
• 无人机堵塞是否合法？城市中噪音呢？旅游行业呢？
• 天气情况怎么样？很难进行天气预测，那么如何进行排期呢？

几分钟内，你就会成为关注的中心，一面是比你了解更多的理论家，另一面是未能得到想要的解决方案的经理们。你的现实生活方法会解决这些问题。

一个万无一失的方法是实践的三维方法：

• 成为一个主题专家（subject matter expert (SME)）：如果理论家极客想出了一百个Google DeepMind TensorFlow函数来解决无人机路线问题，现在你知道如果将现实生活中的参数考虑进来这将是次艰难的航行。SME了解主题，因而能快速认定给定领域中的关键因素。人工智能经常要求找到一个该领域专家都无法以数学方式表达的复杂问题解决方案。机器学习有时表示找到一个人类不知道如何解释的问题的解决方案。深度学习，包括复杂网络，可解决更为复杂的问题。
• 拥有足够的数学知识来理解AI的概念：一旦你拥有适当的自然语言分析，就需要快速创建抽象表达。最好的方式是环顾日常生活并对其创建数学模型。数学不是AI的一个选项，而是一个必要条件。这一努力是值得的。然后，你可以开始编写具体的源代码或开始实现云平台的机器学习方案。
• 了解源代码的功能及其潜能和限制：MDP是一种开始使用三维方法来让我们随机应变的优秀方法：详细地用单词描述周边的事物，将其翻译成数学表达，然后在源代码中实现结果。

第一步 – 自然语言的MDP

任何人工智能问题的第一步是将其转置为日常生活（工作和个人生活）中所了解的事物。对这一事物你是SME。如果你有驾照，那么你就是开车的SME。你有认证。如果你没有驾照或从不开车，就可以将开车替换为步行相关。

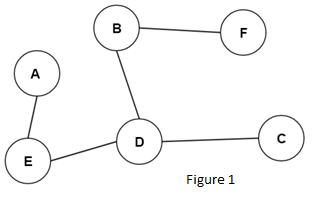
比如你是一个电商业务的司机，在一个你不熟悉的区域投递包裹。你是一个自动驾驶车辆的操作人员。你有GPS系统并在上面有漂亮的彩色地图。你身边的区域以字母A到F表示，如下面的简化图表所示。现在你在F的位置。你的目标是到达区域 C。你很开心，听着收音机。所有事情都很顺利，看起来你将准时到达那里。下图显示了你可能会走过的位置和路线。

导航系统的状态显示了到达 C 的完整路径。它告诉你从F到B到D然后再到C。看起来很棒。

作进一步分解，我们假设：

• 当前的状态是字母s
• 你的下一个动作是字母a(action)。这一动作a 不是位置 A
• 你的下一个动作a（不是位置 A）是去位置不是位置 A。你看着导航系统，并没有堵塞的交通，从你当前的状态F到下一个状态B会花费几分钟。假设下一个状态B就是字母B。

到这里，你还是相当开心，并可以通过以下的一系列事件总结出当前的状况：

字母s是当前的状态、当前所处的情况。字母a是你决定的动作，即到达下一个区域，在那里你进入另一个状态s’。你可以说借助于动作a，你从s进入了s’。

下面，想象一个司机不再是你。出于某种原因你很疲惫。这时自动驾驶车辆就很方便了。你将车设置为自动驾驶模式。现在不是你开车，而是由系统开车。我们称这个系统为代理 。在F这一点，你设置汽车为自动驾驶模式并让自动驾驶代理接管。

代理现在了解了你分配的工作并检查它的地图环境，它表示前图中所示的A到F各区域。

与此同时，你非常的担心。代理是否能完成任务？你在想它的策略是否和你的一样。你有一个策略 P-你思考的方式-即选择最短的路径。代理是否也是这考虑的？它在想些什么呢？你观察并意识到了以前没注意到的事情。因为这你第一次使用这辆车和其导航系统，代理是无记忆的，这是MDP的特性。这表示代理并没知道此前所发生的任何事情 。在区域 F 计算这一状态 s 看起很让人满意。它会使用机器的能力来进行尽可能多的计算来实现目标。

你在观察的另一件事是F到C的总距离来看一切是否 OK。这表示代理在计算从F到C的所有状态。

这种情况下，状态 F 为状态1，我们可以简写为 s₁。B为状态2，可能简写为s₂。D是s₃，C是s₄。这个代理计算所有这些可能的状态来作出决策。

代理知道在到达 D时，C 会更好，因为去 C 比去其它区域的回报更高。因为它不能吃一块蛋糕来回报自己，代理使用的是数字。我们的代理是一个真正的数字饕餮。在错了的时候，它会在模型中获得低回报或无回报。在正确的时候，它会获得以字母 R 表示的回报。这一动作值（回报）转换，通常被称为 Q 函数，它是许多强化学习算法的核心。

在我们的代理从一个状态进入另一个状态时，它执行一个转换并获得回报。例如，转换可以为从F到B，从状态1到状态2或从s₁到s₂。

你感觉很棒并且能按时送达。你开始了解了你的自动驾驶汽车的机器学习代理如何思考。突然你的导航系统瘫痪了。你在屏幕上中只能看到最后一次计算的各区域的静态图像。你向外看，发现交通堵塞正在形成。区域 D 还很远，现在不知道是从D到C比较好，还是从D到E打车走快速通道比较好。你需要你的代理！

代理考虑到了交通堵塞，非常倔强，并增加选择最短路径到达 C 的回报。它的策略是保持原有计划。你不同意，你有其它的策略。

你停下了车。在继续行进之前你们双方需要达成一致意见。你有自己的想法和策略，但是你的代理有不同意见。在继续行进之前，你的观点需要收敛。收敛是确保你们的计算是正确的关键。这种问题是人们之前或者很快自动驾驶车辆之间（更不要说无人机的空中交通堵塞），在整天投递包裹完成工作所会遇到的问题。

在这一点上来表示问题，最好的方式是使用数学表达整个过程。

第二步 – 贝尔曼方程和MDP的数学表达

数学可带来对问题视角的全面改变。你将从单词变成函数这一个源代码的支柱。

以数学标记来表达问题并不意味着要迷失在学术的数学者而不去写一行代码。数学是以完成任务的角度来看待的。跳过数学表达会在一个AI项目早期阶段快速追踪一些函数。但是，在所有 AI 表面发生实际问题时，使用源代码解决这些问题会证实这不太可能。这里的目标是学习足够的数学知识来实现真实世界公司里的解决方案。

有必要通过我们身边所熟悉的事物来思考问题，比如前面讲到的投递日程示例。通过前述那样一些抽象的字母和符号写下来是一件好事，其中a 表示动作，s 表示状态。一旦你理解了问题并以习惯的方式表述了参数，就可以进入下一步。

现在，数学有助于以更短的描述来说明情况。心中有了大体的想法，是时候将它们转化为方程式了。

从MDP到贝尔曼方程

在前面的第一步中，代理从F或状态1或s到B，即状态2或s’。

要这么做，有一个策略-以P来表示的策略。所有这些可以在一个数学表达式MDP状态转换函数中展示：

$$Pa(ss’)$$

P是策略，由代理确定的通过动作 a 从 F 走到 B 的策略。在从 F 到 B 时，该状态转换称为状态转换函数：

• a是动作
• s是状态1 (F)而s’是状态2 (B)

这是MDP的基础。回报（正确或错误）以相同的方式展现：

$$Ra(ss’)$$

这表示 R 是从状态 s 到状态 s’ 动作的回报。从一个状态到另一个状态是一个随机过程。这表示潜在地每个状态都可以进入另一种状态。

我们将要使用的示例会接收一个回报矩阵作为输入，这样程序可以选择这的最佳动作线路。然后代理会从一个状态到另一个状态，学习从每个可能的起点位置的最佳线路。MDP的目标是到达C（回报矩阵的第3行第3列），在以下的 Python 代码是初始值为100.

一些模块以-1开始作为不可能的选项，例如从 B直接走到 C，以值0来定义位置。这一模型以0和1来作为起始。有时会花费数周来设计可以创建回报矩阵的函数（参见第二章 像机器那样思考）。

这一个决策过程有很属性。部分列举如下：

• 马尔科夫属性：在不考虑过往行为会应用这一个过程。对于这一个决策过程像汽车的导航系统那样它是无记忆属性。你向前移动来达成目标。这被称为马尔科夫属性。
• 无监督学习：通过这个无记忆马尔科夫属性，可以放心地说MDP不是监督学习。监督学习表示我们有路线的所有标签。我们确切地知道A的含义并使用该属性来作出决策。我们从将来看过往。MDP不考虑这些标签。这表示它是一个无监督学习。在不知道过去状态或它们代表的含义的情况下进行决策。例如汽车在每个位置都是独立的，由它当时的状态来表示。
• 随机过程：在第一步中，到达状态 B 时，控制测绘系统的代理和司机未能就去哪里达成一致。在试错方式中可以进行随机选择，像掷硬币那样。这将是一个头还是字的过程。代理为掷出数千次并度量结果 。这正是MDP的运作方式以及代理的学习方式。
• 强化学习：重复试错过程并从代理环境获取反馈。
• 马尔科夫链：无历史记录的从一个状态进入另一个状态的随机方式的过程被称为马尔科夫链。

总结一下，我们有三个工具：

• P_a (s,s’)：一个策略，P，或从一个状态进入另一个状态的策略
• T_a (s,s’)：一个 T 或随机转换函数来执行该动作
• R_a (s,s’)：该动作的一个R或回报，可以为负、空或为正

T是一个转换函数，它让代理决定以一个策略从一个点移到另一个点。本例中将为随机。这是机器计算能力的作用，也正强化学习经常被实现的方式。

ℹ️随机是MDP的一个属性

以下代码描述了代理将要作出的决策。

一旦运行了代码，就会选择一个新的随机动作（状态）。

ℹ️贝尔曼方程是对强化学习进行编程的路径。

贝尔曼方程完善了MDP。要计算一个状态的值，我们来使用 Q，作为 A 动作回报（或值）函数。贝尔曼方程的预源代码可以如下方式来表达一个独立状态：

$$Q_{(s)} = R_{(s)} + \gamma*max_{(s’)}$$

源代码然后将等式翻译成一个机器表达，如以下代码：

贝尔曼方程的源代码变量如下：

• Q(s)：这是这一状态-总回报的值。在第一步中代理从F走到B时，驾驶员需要心情愉悦。也许他/她吃了一块糖来让心情愉快，这是人类和回报矩阵的对应。当然可以认为自动驾驶员可以吃下一些电源或可再生能源（回报矩阵）。回报可以是一个数字50或100来向代理显示它走在正轨上。就像学生在考试中获得了一个好的成绩。
• R(s)：这是到那里的汇总值。它是在该点的总回报。
• ϒ = gamma：它在这里提醒我们试错是有代价的。我们在消耗时间、金钱和能源。再者，我们甚至不知道下一步是对还是错，我们处于试错模式。Gamma常被设为0.8。表示什么呢？假设你要考试。你在不断学习，但不知道学习的成果。你可能在80%（0.8）的机会通过。这很痛苦，但这就是人生。这也正让贝尔曼方程和MDP更为真实和有效。
• max(s’)：s’是通过Pa (s,s’)可能达到的一种状态；max是该状态所在行（回报矩阵的位置行）的最大值。

第三步 – 用Python实现解决方案

在第一步中，问题使用自然语言进行描述，来与专家进行讨论并理解预期。第二步中，在自然语言和源代码之前建立了基本的数学桥梁。第三步是软件实现阶段。

在问题出现时-不用担心，这总会发生-会可能回到客户或公司团队的数学桥梁，甚至如有必要更进一步回到自然语言过程。

这一过程保证任意项目的成功。本章的代码使用Python 3.6。它是使用带有如下回报矩阵Q函数的强化学习程序：

R 是数学分析中所描述的回报矩阵。

Q继承了与 R 相同的结构，但因其是一个学习矩阵，所有值均设为0。它会逐步地包含决策过程的结果。变量gamma是再次提醒系统正在学习，并且每次决策仅有80%正确的机会。如以下代码所示，系统在这一过程中探索可能的动作。

例如，代理以状态1开始。你可以选择以任何位置开始，因为它是一个随机过程。注意仅在值 > 0时才予以考虑。它们代表可能的移动（决策）。

当前的状态经过一个分析过程来找到可能的动作（下一个可能的状态）。你会注到没有传统意义上带有多条规则的算法。它仅是随机计算，如以下的random.choice函数所示。

现在来到了包含贝尔曼方程系统的核心，翻译成如下源代码：

你可以看到代理在查找随机选择的下一个可能状态的最大值。

理解它的最好方式是在你的Python环境中运行这程序并print()这些中间值。我建议你打开一个数据表并记录下这些值。这会向你清晰地展示整个过程。

最后一部分仅关乎运行学习过程50,000次，只是要确保系统学习所有可以查找的事物。在每个迭代中，代理会监测当前状态，选择一个动作路径，并更新Q函数矩阵：

在重复了过程之后并直到学习过程结束，程序会打印Q中的结果以及归一化（normed）的结果。归一化的结果是尽可找到的值的汇总除上所有值的过程。结果是一个归一化百分比。

可在 GitHub 仓库查看该 Python 程序

强化学习的课程

无监督强化机器学习，如MDP和贝尔曼方程，会在未来几年颠覆传统的决策制定软件。无记忆强化学习只需要极少甚至不需要业务规则，因此无需人类知识来运行。

成为一个随机应变的 AI 思想者有三个先决条件 – 成为一名SME的努力、处理数学模块、了解源代码的潜能和限制：

• Lesson 1：透过强化学习的机器学习可以在很多用例中打败人类的智能。不用抵抗！技术和解决方案已来。
• Lesson 2：机器学习没有情绪，但你有。你身边的其它人也有。人类的情绪和团队合作是一个重要财富。成为你团队中的SME。学习如何理解他们想要表达的本质内容并为他们制作它的数学表达。这一工作永不过时，哪怕你在配置无需什么开发的Google AutoML解决方案。

强化学习显示人类无法以机器那样的方式解决问题，50,000次随机搜索的迭代不适合人类。模仿人类的神经科学时代已经结束了。廉价、强大的电脑有足够时间计算数百万种可能性并选择最佳路径。

人类会更为直觉，做几种决策并看会发生什么，因为人类无法尝试以50,000种方式来做事。强化学习超越了人类的推理能力，标志着人类思考的一个新纪元。

另一方面，强化学习需要有数学模型来起作用。人类在数学抽象方面非常卓越，向这些强大的机器注意强有力的智力燃料。

人类和机器的边界发生了改变。人类建立数学模型的能力和每个不断增长的云平台会为在线机器学习服务助力。

发现如何使用我们刚刚研究的强化学习程序的输出显示了人类将一直保持人工智能的中心地位。

如何使用输出

我们所研究的强化学习程序像传统软件一样，未包含任何指定领域的迹像。该程序包含带有基于回报矩阵的随机选择的贝尔曼方程。目标是找到一条到达 C 的线路（第三行，第三列），它含有一个诱人的回报（100）：

回报矩阵经过贝尔曼方程并在 Python 中处理结果：

结果包含由强化学习过程所产生的每个状态的值，以及一个归一化的 Q（最大值除以其它值）。

作为Python极客的我们，欣喜若狂。我们处理了相当复杂的工作，名之为强化学习。作为数学的业余人员，我们满心欢喜。我们知道了MDP和贝尔曼方程的含义。

但是作为自然语言的思想者，我们取得了极少的进步。没有客户或用户能读懂这一数据并理解它的作用。再者，我们无法解释我们是如何通过机器实现了他/她的工作的智能版本。我们并没有实现。

我们也不太敢说强化学习通过做了50,000次随机选择最终找到正确答案而打败了公司中的所有人。

还有，我们让程序运行了，但自己却并不知道如何使用这一结果。这一项目的顾问也帮不上忙，因为结果是矩阵格式的。

作为一个随机应变的思考者意味着知道如何在一个主题的方方面面都很出色。要解决这一新的问题，我们先回到结果的第一步。

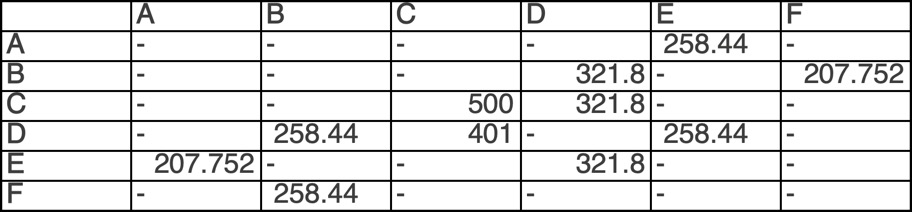
通过图形化工具或数据表格式化 Python 中的结果，结果会显示为如下这样：

这时，我们可以开始阅读这一解决方案了：

• 选择一个起始状态，以 F 为例
• F 行表示它的状态。因为最大值为B列的258.44，我们进入状态 B，在第二行
• 第二行中状态 B 的最大值将我们指向了第四列状态 D
• 状态 D（第四行）的最大值将我们指向了状态 C

注意如果你从状态 C 开始，而又决定不呆在 C，状态 D 成为了最大值，这又会将你重新指向了 C。但是，MDP 不会自行进行这一操作。你需要强制系统来进行这一操作。

现在我们获得了一个序列 F->B->D->C。通过选择其它的出发点，你可以仅通过表格筛选获得其它的序列。

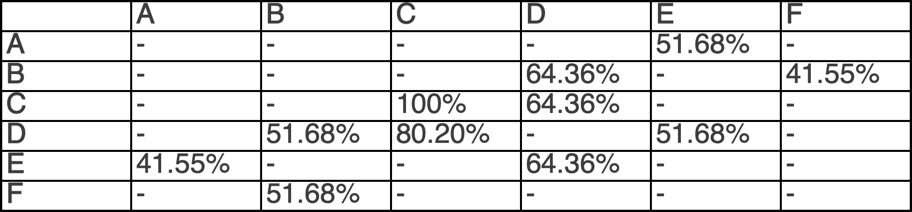
展示它的最有用的方式仍为以百分比显示归一化的版本。这体现了这一个结果的随机属性，生成了其概率而非确定性，如以下矩阵所示：

下面进入了棘手的部分了。我们在本章开始时讲到路上线路的选择。在但结果分析中并没有提及。

强化学习的重要属性为事实上我们处理的是数学模型，可以应用于任何事情上。无需任何人类规则。这表示我们无需编写上千行代码就可以将这一程序用于许多其它主题。

案例1：优化人类或机器驾驶员的投递

该模型在本章中进行了描述

案例2：优化仓库流程

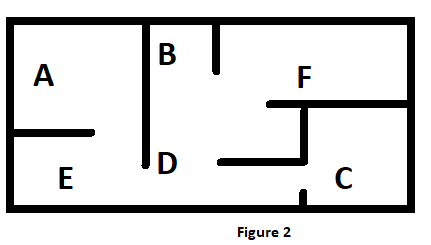
同样的回报矩阵可应用于仓库中从F点到达C点，如下图所示：

在这个仓库中，F->B->D->C 序列在视觉上讲得通。如果有人从F点到达C点，这一物理路径是讲得通的，因为无法穿墙。

它可用于游戏、工厂或任何形式的布局。

案例3：自动规划和调度（APS）

通过将系统转化为调度向量，整个场景就发生了变化。我们离开了更舒适地处理邮件、面孔和路线的现实世界。虽然很迷人，这些应用仅仅是社交的冰山一角。人工智能的真正挑战来自人类思想的抽象世界。

每个独立的公司、个人或系统要求自动规划和调度。本章例中的6个从 A 到 F 的步骤也可以是通过如下向量x以未知顺序展示的6个要执行的任务：

$$x=\begin{bmatrix}
x_{1}\\
x_{2}\\
x_{3}\\
x_{4}\\
x_{5}\\
x_{6}\\
\end{bmatrix}$$

然后回报矩阵体现了要执行的向量 x 任务的约束的权重。例如，在工厂中，你不能在生产零部件之前进行组装。

在这个案例中，该序列获取了体现生产流程的调度。

案例4及更多：你的想像力

通过使用物理布局或抽象的决策制定向量、矩阵和张量，你可以用数学强化模型模型创建一个解决方案的世界。当然，接下来的章节会使用更多其它概念丰富你的工具箱。

机器学习 vs. 传统应用

基于随机过程的强化学习会进化为超越传统的方法。过去，我们会坐下来倾听未来用户来了解他们的思考方式。

然后我们会回到键盘上并尝试模仿这一人类思考方式。那样的日子已成为过去式。我们需要适当的数据集和机器学习/深度学习方程来取得进展。应用数学将强化学习带到了下一个 level。传统软件很快会进入计算机科学的博物馆。

一个人工智能的随机应变思考者通过应用数学翻译成机器展现来看待整个世界。

小贴士：使用本章中提供的不同方式的Python 源代码示例。运行它，尝试修改一些参数来看会发生什么。也可以修改迭代的次数。将50,000减少到你发现为最佳的次数。微调回报矩阵来看会发生什么。设计你自己的回报矩阵路径。它可以是一个日程或决策制定过程。

总结

现在，人工智能是应用数学占主导地位的分支，而非神经科学。你必须掌握线性代数和概率论的基础。这对于习惯于直觉创意的开发者是一种困难。通过这一知识，你会发现人类不是拥有 CPU 和数学方程的机器的对手。你也会了解到机器与你身边的宣传不同，并不具备情绪，虽然我们可通过聊天机器人可以将其展现到让人毛骨悚然的程序（参见第十四章 加强聊天机器人的情感智能缺陷）。

说了这此，多维方法是AI/ML/DL项目的先决条件 – 首先讨论项目并写下，然后制作一个数学展现，并最后进入软件生成（配置已有平台并/或编写代码）。在现实生活中，AI 解决方案不会树那样在公司中自发生长。你需要与团队讨论并一起协作。这部分是真实的实现项目的一面 – 首先进行想象，然后与真实世界的人们一起实现它。

MDP，一个由贝尔曼方程增强的随机动作回报（值）系统，会为许多 AI 问题提供有效的解决方案。这些数据工具可以完美融入公司环境。

使用Q动作值的强化学习是无记忆的（没有过去）并且是无监督的（数据未被打标签或分类）。这样会节约开发让系统运作的规则的很多个小时，来提供解决现实生活问题的无尽途径。

既然我们已经处于Google DeepMind方法的核心，是时候进入第二章 像机器那样思考并透过讲解和源代码发现首先要如何创建回报矩阵。

喜欢 (2)赏

[]

分享 (0)